基于宏程序的非圆曲线最短加工路线设计.pdf 3页

2013年5月机床与液压Mav2013第41卷第10期MACHINETOOL&HYDRAULICSVo1．41No．10DOI：10．3969／j．issn．1001—3881．2013．10．017基于宏程序的非圆曲线最短加工路线设计冯大鹏，黄耀威(佛山科学技术学院，广东佛山528000)摘要：通过实例探讨了具有最短切削路线的非圆曲线的加工方法。设计一种矩形循环进给路线，实现非圆曲线加工循环，使加工路线较短，效率提高。关键词：宏程序；非圆曲线；最短切削路线中图分类号：TH164文献标识码：B文章编号：1001—3881(2013)10—050—3TheShortestProcessingRouteDesignforNon-circularCurveBasedonMacroProgramFENGDapeng，HUANGYaowei(FoshanUniversity，FoshanGuangdong528000，China)Abstract：Theprocessingmethodtorealizetheshortestroutefornon—circularcurvewasinvestigatedbyexample．Therectangleloopwasdevisedtoachieveprocessingcyclefornon—circularcurve，whichmadethecuttinglineshortenandNCeficientimprove．Keywords：Macroprogram；Non—circularcurve；Theshortestprocessingroute在非圆曲线轮廓的轴类的数控加工编程中，宏程在切削过程中，切削进给路线长短与切削方式有序具有独特的优势。手工常规编程无法编制出非圆曲关。对工件某切削区域的粗加工，一般有两种切削进线加工程序，而应用宏程序，可通过变量赋值、运算给路线选择：(1)平行轮廓的等距路线；(2)平行等变化，形成插补的更新，用细段直线逼近轮廓线，坐标轴的“矩形”走刀路线。这两种切削路线的长并自动完成下一接点的计算及插补运动，从而完成非短是不同的，下面可通过实例对比进行分析。圆曲线加工。粗加工时，宏程序所形成的切削路线为图1所示斜线n为粗加工完成后的轮廓线，而a轮廓等距线，按同一轨迹重复切削，每次切削刀具向为o的等距线。加工a以下区域有两个方案：(1)前移动一次，直至加工完成。这种循环进给路线是由平行a进行切削，其刀路如图1虚线所示，分n次走于宏程序的特点而形成的，它与常用的复合车削循环刀完成，背吃刀量为b／n；(2)走平行坐标轴的矩形指令G70、G71的刀具路线相差较大，而与仿形复合循环进给路线，其刀路如图1实线所示。粗加工最后粗车循环指令G73所形成的刀具路线相仿。从刀具一刀轨迹相同。路线优化角度来看，这种走刀方式的加工效率有待提高。1沿坐标轴平行切削是实现最短进给路线的有效方法使加工程序具有最短的走刀路线是优化加工程序的主要目标之一。走刀路线是指切削加工过程中刀具相对于被加工零件的运动轨迹，它包括参与切削和不参与切削两大部分，其中不参与切削部分指空程走刀路线。对于如何减少走刀空程，特别是减少进给走刀空程的研究，已经有较多的论述。但对于参与切削部图1两种切削进给路线分的刀具路线，如何实现优化设计，其研究还有待深由图1可得：入，其目的在于使切削进给路线最短，减少切削加工时间。收稿日期：2011—04—03作者简介：冯大鹏(1957一)，男，高级工程师，主要研究方向为数控加工。E—mail：fsfdp@126．com。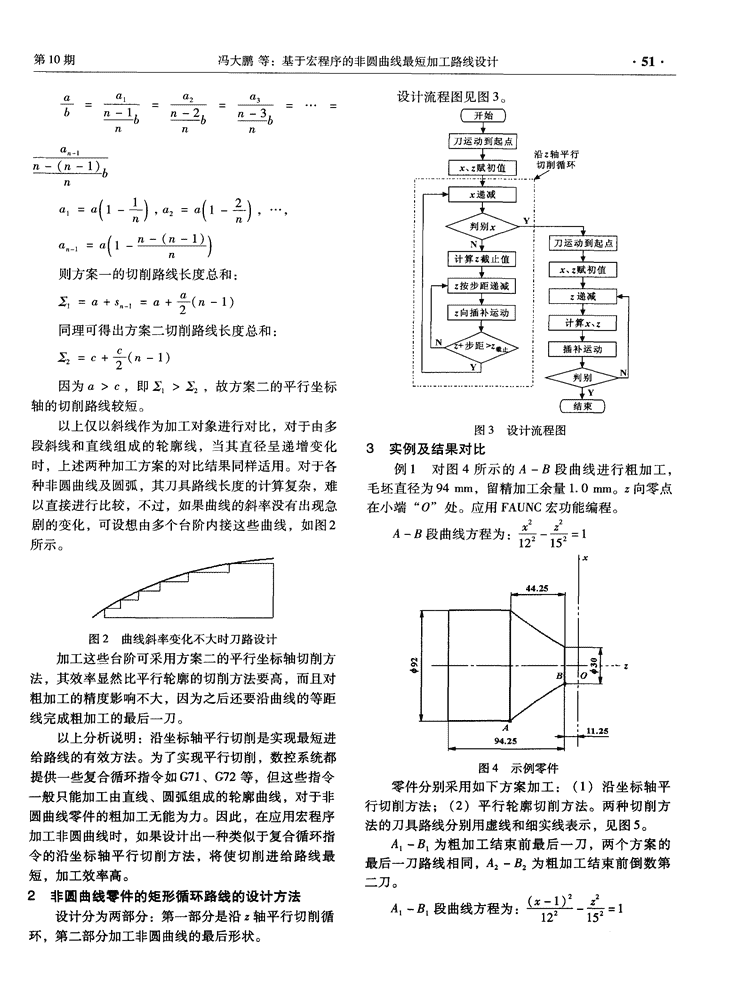 第10期冯大鹏等：基于宏程序的非圆曲线最短加工路线设计·51·a设计流程图见图3。一一兰竺：⋯：：b66n：二(二a1=n(一1)，a2=。(t—2)，⋯，an_l=nf1一1则方案一的切削路线长度总和：1=口+s1=0+。(n一1)一同理可得出方案二切削路线长度总和：乏=c+，_(n一1)因为a>C，即>，故方案二的平行坐标轴的切削路线较短。以上仅以斜线作为加工对象进行对比，对于由多图3设计流程图段斜线和直线组成的轮廓线，当其直径呈递增变化3实例及结果对比时，上述两种加工方案的对比结果同样适用。对于各例l对图4所示的A—段曲线进行粗加工，种非圆曲线及圆弧，其刀具路线长度的计算复杂，难毛坯直径为94mm，留精加工余量1．0mm。向零点以直接进行比较，不过，如果曲线的斜率没有出现急在小端“O”处。应用FAUNC宏功能编程。22剧的变化，可设想由多个台阶内接这些曲线，如图2A—B段曲线方程为：号一=1所示。44．25——图2曲线斜率变化不大时刀路设计＼加工这些台阶可采用方案二的平行坐标轴切削方法，其效率显然比平行轮廓的切削方法要高，而且对B粗加工的精度影响不大，因为之后还要沿曲线的等距线完成粗加工的最后一刀。．／以上分析说明：沿坐标轴平行切削是实现最短进94．25’给路线的有效方法。为了实现平行切削，数控系统都图4示例零件提供一些复合循环指令如G71、G72等，但这些指令零件分别采用如下方案加工：(1)沿坐标轴平一般只能加工由直线、圆弧组成的轮廓曲线，对于非行切削方法；(2)平行轮廓切削方法。两种切削方圆曲线零件的粗加工无能为力。因此，在应用宏程序法的刀具路线分别用虚线和细实线表示，见图5。加工非圆曲线时，如果设计出一种类似于复合循环指A一为粗加工结束前最后一刀，两个方案的令的沿坐标轴平行切削方法，将使切削进给路线最最后一刀路线相同，A：一：为粗加工结束前倒数第短，加工效率高。二刀。2非圆曲线零件的矩形循环路线的设计方法A。一B。段曲线方程为：一=l设计分为两部分：第一部分是沿z轴平行切削循环，第二部分加工非圆曲线的最后形状。 ·52·机床与液压第4l卷GOX94Z—l1．25A一B：段曲线方程为：主一互152=l#3=32／／切削余量变量赋值N2G0X94Z—l1．25#3=#3—2．0／／切削余量递减IF[#3LE0]GOTO5／／~tl断切削余量l，口、#1=一l1．25／／Z变量赋值N4#2=SQRT[144$[1+#1#1／225]]+1／／计算X、G01X[2[#2+#3]]Z#1F120／／直线插补#1=#1—0．5／／Z值递减图5两种切削方法的刀路柏=2：I=[}}2+#3]IF『拍LT94]GOTO4／／刀是否超出毛坯(1)沿坐标轴平行切削方法。设：样1为z变量，}}2为z截止变量，#3为x变量。GOT02N5GOX94Z一11．2500001M30$400M3TO101两种方案的刀具路线长度总和(A一B：以下部G0X94Z一11．25位)见表1。表1两种方案的刀具路线长度总和#3=48／／X变量赋初值N2G0U2／／退刀方案刀具路线长度总和／mmGOX94Z．11．25沿坐标轴平行切削318．7#3=#3-2．0／／X变量递减平行轮廓切削438．2IF[#3LE18．0]GOTO5／／N断x变量从表1可知：采用方案一切削路线明显缩短，这#1=一11．25／／Z变量赋初值对于提高加工效率有较大帮助。#2=SQRT[225[[#3—3][#3—3]／144—4结束语1]]／／计算z截止值通过设计一种近似于矩形的循环进给路线，实现N4#1=群1—0．5／／Z值递减粗加工垂直进刀一水平切削一退刀一再进刀的加工循G01X[2$]Z#1FIO0／／直线插补环，使加工路线较短，效率提高。这种加工方法对于IF[[#1]IJT]GOTO2／／N断z值是否到截止值单调变化的非圆曲线，如双曲线、对数曲线等的加工G0TO4非常有效，而对于非单调变化的非圆曲线加工，单一N5GOX94Z一11．25／／准备加工A1一Bl段的矩形循环进给路线并不适用，此时需要采用平行#1=一11．25／／Z赋初值轮廓的等距路线，其优点是节省了换刀时间，一次加N6#3：SQRT[144：l：[1+#l$#1／225]]+1／／计算工完成。但由于零件外圆含有凹弧，为避免刀具副切X削刃与工件发生干涉现象，刀具副偏角一般较大，而GO1X[2$#3]Z#1FS0／／插补运动副偏角加大不利于刀具强度的提高和加工散热，影响#1=#l一0．2／／Z递减刀具寿命，同时限制了切削用量，不利于加工效率的IF[拌1GT一55．5]GOTO6／／~1]断z值是否到终点提高。从优化加工路线角度综合衡量，需寻找更加合GoX94Z一11．25理的加工方案的配对组合。M30参考文献：(2)平行轮廓切削方法。【1】王娟平．回转体类零件的数控加工工艺路线及工序进给设：#1为z变量，#2为x变量，#3为切削余量变路线的设计[J]．新技术新工艺，2011(6)：56—58．量，拍为中间变量。【2】陈光明．数控加工中工艺路线设计原则及方法[J]．组00002合机床与自动化加工技术，2005(11)：69—72S400M3I10】