- 2.91 MB
- 2022-05-11 18:36:38 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
第九章架空线的断线张力
和不平衡张力架空输电线路设计
第一节概述1、定义断线张力:因架空线断线,断线档的相邻档架空线所具有的残余水平张力,称为架空线的断线张力。不平衡张力:因气象条件变化,在直线杆塔上产生的水平张力差,称为架空线的不平衡张力。2、目的(1)计算杆塔强度;(2)验算架空线与杆塔的电气间隙;(3)校验被跨越物间距;(4)检查转动横担或释放线夹是否能动作。
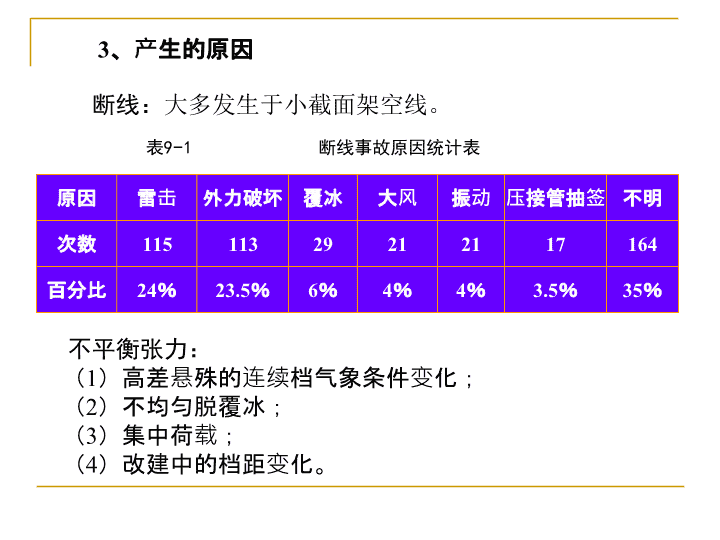
3、产生的原因原因雷击外力破坏覆冰大风振动压接管抽签不明次数11511329212117164百分比24%23.5%6%4%4%3.5%35%不平衡张力:(1)高差悬殊的连续档气象条件变化;(2)不均匀脱覆冰;(3)集中荷载;(4)改建中的档距变化。表9−1断线事故原因统计表断线:大多发生于小截面架空线。
4、确定方法(1)设计杆塔时:规定断线张力取最大使用张力的百分数作为杆塔校验荷载。(具体杆塔设计课程中讲述)(2)计算电气间距时:依据实际档距、高差、杆塔结构和气象条件,采用公式具体计算。(重点研究)
第二节固定横担固定线夹下
单导线的断线张力1、断线张力是断线冲击过程稳定后的已经衰减了的“残余张力”。2、影响断线张力大小的因素:(1)绝缘子串越长,导线就越松弛,张力衰减就越多,残余张力就越小。(2)直线杆塔产生绝缘子串偏斜方向的挠曲变形,增大了导线的松弛量,残余张力因而更小。(3)断线引起的绝缘子串偏斜和杆塔挠曲变形,还使未断线侧各档的档距向减小的方向变化。紧邻断线档的档距减小得最多,距断线档越远减小得越少。(4)断线张力的大小与断线后剩余的档数有关。一般情况考虑五档。(5)未断避雷线的支持力。一、断线张力的特点当高压架空线路跨越铁路、公路、电车道、弱电线路以及特殊管道时,需要校验邻档断线后导线对交叉跨越物的距离,因而需要计算断线张力。
一、断线张力的有关方程及其求解1、档距减小量与应力的关系断线前气温为t,比载γ,各档水平应力为σ0,第i档的档距为li0,高差角βi0。断线后气温、比载不变,第i档档距减小了△li变为li,水平应力变为σi0,仿公式(8−19),略去高差变化量的影响,断线后第i档的档距减小量为(9−1)用张力表示为(9−2)
断线后由于架空线张力变小,弹性伸长量也减小,故断线后档内悬线长度要比断线前缩短一些。断线后档距缩小,△li取为正。若断线后连续档剩余k档,则依式(9−2)可列出k个方程,但含有Ti、△li(i=1,2.,…,k)共2k个待求量,需再列出k个方程才能求解。2、悬挂串偏移量与两侧张力的关系:设悬垂串悬挂点处的杆塔挠度系数为B,可写出架空线悬挂点偏距δi的计算式为(9−3)
利用式(9−2)、(9−3)两组方程,按下面步骤试凑求解:设已知T1→式(9−2)→△l1;δ1=△l1;δ1、T1→式(9−3)→T2;T2→式(9−2)→△l2;δ2=δ1+△l2;δ2、T2→式(9−3)→T3;……;Tk→式(9−2)→△lk;δk=δk−1+△lk;δk、Tk→式(9−2)→Tk+1≡0。利用上述方法试凑求解时,初值T1(△l1)的取值对计算的反复次数影响很大。残余张力T1一定小于未断线前的张力T0=σ0A。剩余档数越多,T1与T0的差值越小,档距的变化量△l1也越小。
二、求解断线张力的作图法利用计算机采用试凑法求解断线张力是很方便的。在无条件应用时,可采用图解法。具体作法如下:(1)以δ(△l)为横坐标,T(△T)为纵坐标建立直角坐标系,如下图。(2)利用式(9−2),绘制断线后各档档距变化与张力变化的关系曲线Ⅰ:T=f(△l)(3)利用式(9−3),绘制断线后直线杆塔上架空线悬挂点偏移量δi与不平衡张力差△Ti=Ti−Ti+1的关系曲线Ⅱ:δ=f(△T)。
(4)图解法求解步骤假定靠耐张塔一档的架空线张力为T1,由T1查曲线Ⅰ中相应曲线1,得到△l1。因δ1=△l1,据此查曲线Ⅱ中相应曲线1,得到△T1,计算出T2=T1−△T1。由T2查曲线Ⅰ中相应曲线2得到△l2,算出δ2=△l2+δ1。由δ2查曲线Ⅱ中相应曲线2,得到△T2,算出T3=T2−△T2。由Ti查曲线Ⅰ中相应曲线i得到△li,算出δi=△li+δi−1。由δi查曲线Ⅱ中相应曲线i,得到△Ti,算出Ti+1=Ti−△Ti。如此类推下去,直至算出断线相邻档的Tk,由Tk查曲线Ⅰ中相应曲线k,得到△lk,算出δk=△lk+δk−1,由δk查曲线Ⅱ中相应曲线k,算出△Tk。
三、断线档的选择原则为保证交叉跨越在断线事故情形下,满足规程规定的跨越限距要求,断线档应选在跨越档的相邻档,不同档距分布下的断线档选定原则见下表。如果Tk>△Tk,或者说δk线末端P点未到达曲线Ⅱ中相应曲线k,表明T1设大了。如果Tk<△Tk,或者说δk线末端P点超过曲线Ⅱ中相应曲线k,表明T1设小了。如果Tk=△Tk,或者说δk的线段末端P正好落在曲线Ⅱ中相应曲线k上,则假定的T1正确,Tk即为所的断线张力。否则应重新假定T1,重复上述步骤直至Tk=△Tk为止。
档距分布形式档距特点断线档选择各档档距大致相等选在档距较多的一侧断线。跨越档两侧的档距分别为一大一小,即l3>l5。选在大档距内断线。跨越档两侧的档距一侧较大,一侧很小,且小档距的邻档为一大档距。l2>l5>l3先选在较大档距l5内断线,若计算结果裕度不大,需再选在小档距内断线计算,取裕度小的情况。跨越档一侧为大档距,且靠近非直线杆塔。l1>l3先假定选在多档距一边,再计算大档距一边。表9−4断线档选取原则一览表
【例9−1】某35kV架空输电线路,无地线。一耐张段内共有10档,档距基本相等,代表档距为lr=273m,如图所示。导线截面积为A=146.73mm2。在档距l8内跨越Ⅰ级通讯线,通讯线高7m,位于距8号杆30m处。直线杆塔悬点高13m,挠度系数B=0.0003m/N。悬垂串长=0.886m,重233.4N。设气温+15℃、无风、无冰时架空线应力为σ0=75MPa,自重比载γ1=35.2×10−3MPa/m。试核验邻档断线后的交叉垂直距离。
【解】欲核验跨越间距,应选取邻档断线进行计算。因断线后剩余档数越少,张力衰减越严重,松弛弧垂越大,所以取档距l7为断线档。(1)作T=f(△l)曲线Ⅰ:给出不同的T,可求得相应的△l,数据示于表9−5中,曲线Ⅰ绘制于图9−4中。(m)T(N)2500300035004000450050005500△l(m)3.5012.4541.8071.3781.0760.8560.690T(N)60006500700075008500950011004.75△l(m)0.5600.4560.3710.3000.1870.1000
(2)作δ=f(△T)曲线Ⅱ因各档距基本相等,垂直档距lv等于水平档距lh,则悬垂点的垂直荷载将有关数值代入式(9−3),得给出不同的△T,求出相应的悬点偏移量δ,如表9−6。利用该组数值作出图9−4中的曲线Ⅱ。(N)(m)△T(N)2505007501000150020002500δ(m)0.21820.42580.61570.78551.07091.30431.5062△T(N)3000350040004500500055006000δ(m)1.68961.86212.02782.18902.34742.50372.6586
(3)按照作图法的步骤,根据图9−4,求得各档导线的残余张力、直线杆塔承受的不平衡张力以及悬挂点偏移量,列于表9−7。导线残余张力(N)不平衡张力差(N)悬点偏移量(m)T7T8T9T10ΔT7ΔT8ΔT9δ7δ8δ90441359076450441314595562.151.050.47
(4)核验交叉垂直距离由于断线张力T8=4413N,所以断线应力为跨越点处导线的弧垂为导线对Ⅰ级通讯线的交叉距离为S=13−7−4.265=1.735(m)由规程知,该电压等级的输电线路,断线时对Ⅰ级通讯线交叉跨越距离应不小于1m,故本例满足要求。(MPa)(m)
第三节分裂导线的断线张力分裂导线一相导线全断的机率很小,即使考虑一根次导线断线,但由于未断次导线的支持,杆塔上产生的不平衡张力也往往小于线路正常运行和施工紧线时杆塔上出现的最大不平衡张力。设有n根次导线,耐张段内有连续m档,各档等高等档距,档距为l0,断线前每根次导线的水平张力为T0,悬垂串长,重GJ,第k档相导线断线后尚剩n’根次导线。当一相内有次导线断裂时,一般认为断线档内的间隔棒被拉脱或损坏,故不承受张力差,即张力差全部作用在悬挂点上。
断线后断线档的档距及剩余n‘根次导线的张力均要增加,其它档的档距及张力均减小。设断线后第i档每根次导线的张力Ti,档距变化量△li与每根导线张力Ti的关系,仍可用式(9−2)表示。
分裂导线断线后,剩余次导线的支持力使杆塔的刚度大为增强,因此可以忽略杆塔的挠曲变形。断线档的非相邻档的悬挂点偏移量δi与两侧每根次导线的张力差△Ti的关系为(9−4)断线档两侧直线杆塔上的悬垂串偏移量δk−1、δk与其两侧每根次导线的张力Tk、Tk+1的关系为(9−5)(9−6)
各档档距改变量△li与悬点偏移量δi的关系为根据上述各公式即可采用试凑法或图解法求解,方法同上节。(9−7)
第四节线路正常运行中的不平衡张力直线杆塔承受不平衡张力的几种情况:(1)耐张段中各档距长度、高差相差悬殊,气象条件变化引起各档张力不等。(2)耐张段中各档不均匀覆冰或不同时脱冰,因各档比载不同引起张力不等。(3)线路在检修时,采取先松下某悬点的导线或后挂某悬点的导线,造成两档合为一档,将引起与相邻各档张力不等。(4)耐张段某档进行飞车、绝缘爬梯等作业,集中荷载引起不平衡张力。(5)在高差很大的山区,尤其是重冰区的连续倾斜档,山上档和山下档的张力不等。计算方法:连续档的精确计算
第五节地线的支持力断导线时,断线张力使悬垂串偏斜,杆塔挠曲,杆塔顶部地线的悬挂点产生位移,地线在断线档被拉紧,起到限制杆塔挠曲的支持作用,此时的断线档的地线张力称为地线的支持力。地线的支持力与耐张段的长度、档距大小及断线档的位置有关。对柔性直线杆塔(如无拉线的直线单杆和门型杆),地线的支持力可达导线断线张力的40~70%,对杆塔及基础设计的影响不可忽略。一、地线支持力对杆塔的作用断线档两侧的直线杆塔上作用有导线的不平衡张力△Td和地线的支持力△Tb,二力的作用方向相反,如图(a)所示。
杆塔可视为一端自由、一端固定的悬臂梁,其弯矩图(b)。曲线1、2分别是地线最大支持力和最小支持力情况下杆塔的弯矩。可以看出,地线支持力最小时,杆塔的弯矩在地面处最大,所以计算杆塔根部受弯和基础倾覆时,需用最小的地线支持力。地线支持力最大时,横担处的弯矩最大,所以计算横担受弯受扭时,需用最大的地线支持力。
二、地线支持力的计算1、假设(1)忽略非断线档直线杆塔上导线不平衡张力引起的杆顶挠度;(2)不考虑导线不平衡张力与地线支持力的相互影响。(3)耐张段的第n+1档导线断线,导线的断线张力已经求得,需确定地线对n号杆塔的支持力。
2、杆顶挠度系数断线张力和地线支持力作用下的杆顶挠度系数Bd和Bb,可分别由下二式计算(9−9)(9−10)杆塔根部嵌固处的刚度与作用力位置有关的系数地线线夹悬挂点距杆塔根部嵌固处(一般取埋深的1/3)的高度(m/N)(m/N)
3、求地线支持力△Tb(1)假定地线支持力△Tb:n号杆塔上地线线夹的位移为(9−11)n号杆地线线夹的位分别为导线断线张力△Td和地线支持力△Tb引起的杆顶位移地线悬垂串的偏移量导线断线张力地线的支持力地线悬垂串长地线作用于悬垂串上的垂直荷载地线悬垂串的重量(2)求第n+1档地线的张力Tn+1若n+1号杆为耐张杆,则该档档距将增加△ln+1=δn。若n+1号杆为直线杆,位于耐张段的中部:△ln+1=2δn。设断线前后气温相同,地线比载不变,相应集度为p,第i档水平张力分别为T0、Ti,仿式(9−2)得地线张力与档距变化量△li之间的关系为
(9−12)在确定△ln+1后,第n+1档地线的张力由下式确定(9−13)按上式计算时,应判别△ln+1之正负。断线档的档距增大,△ln+1应为正值。(3)求第n档地线的张力TnTn应为整个耐张段中地线张力最小的,并小于断线前的地线张力T0。
(4)第n档的档距变化量△ln利用公式(9−12),算得△ln(△li,i=n、n−1、…2、1)。△li应为负值,因为非断线档的档距减小。(6)第i基杆塔的地线张力差(9−15)该式适用于自第n−1基开始递减的杆塔,式中第二项为地线张力差引起的杆顶挠度,对某些类型的杆塔(如拔梢杆)而言,其值影响甚大。(9−14)(5)非断线档的地线线夹位移与档距变化量的关系
(8)第i档地线的张力(9−16)(9)返步骤(4)反复进行计算,直至0号耐张杆塔为止,此时应有δ0=0。如果δ0≠0,则应修正原假设△Tb,重新计算,直到满足要求为止。
某110kV架空线路,导线为LGJ−95/20,某耐张段共有10档,无高差,档距基本相等为lr=250m,在档距l7内跨越Ⅰ级通讯线,靠输电线路档距中央侧的通讯线高7m,位于距6号杆40m处,如图所示。直线杆塔悬点高14m,挠度系数B=0.0003m/N,悬垂串长=1.322m,重393N。在气温+15℃、无风时的导线应力为σ0=66MPa,试核验邻档断线后的交叉垂直距离。作业题
您可能关注的文档
- 建筑电气中供配电线路设计研究.pdf
- 对山区公路线路设计的若干思考.pdf
- 亚的斯亚贝巴轻轨项目线路设计.pdf
- 某公司企业网络线路设计.doc
- 关于城市轨道交通线路设计发展方向的探讨.pdf
- 旅游设计论文:旅游与线路设计的重要性.doc
- 题库输电线路设计题库2013.04.17.doc
- 题库输电线路设计题库.doc
- 数学建模送货线路设计问题 答案仅供参考.doc
- 旅游线路设计 .ppt
- 星座主题旅游线路设计.ppt
- 最新10kV线路设计.ppt
- 架空线路设计全解.ppt
- 旅游线路设计原则.doc
- 电子线路设计报告材料.doc
- 电子线路设计报告.doc
- SDJ 206-87架空配电线路设计技术规范.pdf