《架空输电线路设计讲座》第10章解析课件.ppt 47页

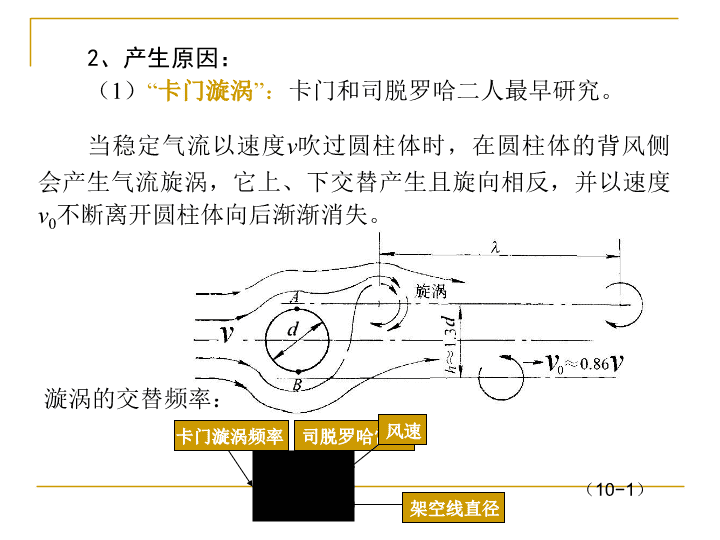
第十章架空线的振动和防振架空输电线路设计 第一节架空线的振动形式及其产生原因振动形式：由风雪引起：微风振动、舞动、次档距振动、脱冰跳跃和摆动；由电磁力引起：短路振动和电晕振动。一、微风振动微风振动是架空线在微风作用下产生的高频低幅的垂向振动。1、特点：微风、高频、低幅、长期。该类振动所需风速较小，通常在0.5～10m/s范围内；振动频率较高，5～120Hz；振幅不大，一般为架空线直径的3倍以下；持续时间较长，一般为数小时，有时可达几天。 当稳定气流以速度v吹过圆柱体时，在圆柱体的背风侧会产生气流旋涡，它上、下交替产生且旋向相反，并以速度v0不断离开圆柱体向后渐渐消失。2、产生原因：（1）“卡门漩涡”：卡门和司脱罗哈二人最早研究。漩涡的交替频率：（10−1）司脱罗哈常数卡门漩涡频率架空线直径风速 （2）固有频率：fn（2）共振：fs=fn（4）同步效应或锁定效应：风速发生变化不超过某一范围，架空线的振动频率和漩涡频率都不变化，仍保持为架空线的固有频率fn，这种现象称为同步效应或锁定效应。3、危害：引起架空线疲劳断线、金具磨损和杆塔部件破坏等。 二、舞动1、特点：低频、大幅、中风。2、产生原因（1）垂直舞动机理:美国Den.Harton提出：偏心覆冰时，月牙形的覆冰形成机翼，作用于其上的风力分解为水平分力和垂直分力，垂直的气动升力大于导线的气动阻力时导线发生舞动。（2）扭转舞动机理:加拿大O.Nigol提出：架空线有上下运动，又有扭动，当横向垂直振动频率与架空线固有扭转频率耦合时，产生舞动。（3）动力稳定性机理:该理论把舞动看作为一种动力不稳定现象，考虑了垂直、水平和扭转分量以及三者的耦合。（4）低阻尼系统共振机理:低阻尼条件下，由风力产生的结构共振。较好地解释薄冰（无冰）导线也产生舞动的现象。可以肯定：风是舞动的必要条件，冰是舞动的主要因素。振荡起来势如野马奔腾，称为奔马型振动。频率低（0.1～3Hz）、振幅大（一般为米数量级，可达10ｍ以上），多在导线覆冰、气温0℃、且有强风（10～20m/s）时发生。舞动一般较少发生，但一旦发生，持续时间较长，常为数小时。架空线截面积较大（直径＞40mm），分裂导线根数较多，架空线离地较高时较易舞动。3、危害：引起导线鞭击，损坏金具，造成线间闪络，使线路跳闸，甚至会烧伤导线或引起断线，造成大面积停电等严重事故。4、防止舞动措施：避舞、抗舞和抑舞。 三、次档距振动1、特点：频率为1～5Hz，振幅介于舞动和微风振动之间，为架空线直径的4～20倍。2、原因：同一相中有多条导线，迎风导线的尾流效应，会使下风头导线受其影响而产生上扬力，使之产生振动。次档距振动（振荡）是风的尾流效应引起的子导线在次档距内的水平振动，图示了4分裂导线的典型次档距振动。3、危害：分裂导线相互撞击而损伤导线，导线在间隔棒线夹处产生疲劳断股，使间隔棒线夹松动。4、解决措施：采用阻尼间隔棒，增大分裂导线的间距，缩短次档距长度，合理布置子导线位置等。 四、脱冰跳跃型振动1、特点：脱冰跳跃。2、危害：上下导线相间短路。3、解决措施：保证在垂直方向错开足够距离。五、受风摆动型振动1、特点：在θ−α与θ+α之间不同步摆动。2、危害：会引起相间闪络。3、解决措施：加长横担以增大导线间距。六、短路电流引起的导线振动电磁力作用下同相的几根导线相吸或相斥。切断电流后，导线又在自重和拉力作用下作相反方向的运动。七、电晕引起的振动导线下面附着水珠时，会引起电晕放电。随着电晕现象的激化，将带电水珠的微粒子射出，反作用使导线受到向上的力。反复作用，引起有规律的振动。 第二节微风振动的基本理论某档距架空线如图，在无刚度无阻尼的情形下，略去自重，对微段dx，其受力情况如图所示，其中为运动惯性力。单位长度质量为m设档距为l水平张力为T0一、无刚度无阻尼的架空线振动 1、列出平衡方程式为（a）（b）代入式（b），有即（10−2）、、、将 采用分离变量法求解，设（10−3）代入（10−2）中，得（c）令，则（d）上式左端与t无关，右端与x无关，因此必等于同一常数。令这个常数为，则（e） 于是（10−4）其解为（f）（g）U（x）是位置x的函数，称为主函数。将上二式代入式（10−3），得（10−5）式中常数A、B由边界条件确定，C、D由初始条件确定。 2、导线两端固定：则当x=0时，y（0，t）=0；x=l时，y（l，t）=0。代入式（f），得B=0和sin（ωl/a）=0，由后者知（n=1，2，3，…）（10−6）（n=1，2，3，…）上式中的ωn为架空线的固有圆频率，不同的n表示不同阶的固有圆频率。以固有振动频率fn表示（10−7）其中λ为振动波波长（10−8）从式（10−7）可以看出，导线的固有频率只与n、l、T0和m有关，是由系统所决定的，与初始条件无关。对应不同的n，有不同的频率fn，即固有频率不是一个值，而是一组值。 将式（10−6）和B=0代入式（f），得主函数为：（n=1，2，3，…）（10−9）上式是n阶固有频率的振动主模态，在架空线长度方向上呈正弦曲线变化。所以（10−10）假设导线的初始位移为零，即当t=0时，代入式（10−10）得（h）必有所以（10−11）距架空线悬挂点的水平距离最大振幅以圆频率ωn振动时的波长 相应的线上各点的速度为（10−12）各点的加速度为（10−13）从式（10−11、12、13）看出，位移、速度、加速度都是时间的正弦函数，它们的变化周期相同，只是相位不同。速度超前位移90°，加速度超前或滞后位移180°，即与位移方向相反。 从看出，当n=1时，x从0到再到l变化时，从0到1再到0，是一个正弦“半波”。当n=2时，x从0到再到变化时，从0到1再到0，是一个正弦“半波”；x从到再到l变化时，从0到－1再到0，是又一个正弦“半波”。所以n代表档内的半波数。导线振动时，档内可以有一个半波，直到无穷多个半波。（2）架空线上的某点作简谐振动。对某一确定位置x0，有（1）分析： 上式表明，架空线上的某点作简谐振动，振幅。当（k=0，1，2.，…）时，yx=0，这样的位置称为节点。当时，振幅达到最大，这样的位置称为波腹。所以振动波沿档距呈正弦的驻波分布，波节点、波腹的位置不变，其振幅为（3）沿档距呈正弦的驻波分布。对某一确定时刻t0，有 设架空线的刚度为EJ，水平张力为T0，单位长度质量为m。由于刚度的存在，微元段dx上有弯矩，如图所示。列平衡方程有：二、有刚度无阻尼的架空线振动 整理之，得（a）（b）由梁的弯曲理论代式（c）入式（b）（c）（d）代入式（a）（e） 用分离变量法解此偏微分方程，设，代入式（e）得（f）上式左边为x的函数，右边为t的函数，左右两边必等于同一个常数。设这个常数为，可得到两个常微分方程（g）和式（h）的解为（h）（i） 假设导线两端为铰支，则当时，；当，。设（n=1，2，3，…）（j）能满足边界条件，将U（x）代入式（g），有所以（10−14） 将式（i）、（j）代入，得到主模态的位移方程（10−15）式中常数An、Bn，根据初始位移和初始速度确定。将有刚度架空线的固有频率与无刚度的比较，其比值为：刚度架空线的固有频率比无刚度的稍大，固有频率的阶数越高二者相差得越多。（10−16） 第三节影响微风振动的主要因素一、风速和风向的影响风作用于架空线上，输入一定的风能，使其发生振动。输入的能量与风速平方成正比。风速较小时，输入的能量不足以克服架空线系统的运动阻力，因此引起架空线振动的风速有一下限值，一般取0.5m/s。当风速增大及其不均匀性增加到一定程度时，由于卡门旋涡的稳定性受到破坏，致使架空线振动减弱甚至停止，因此振动风速有一上限值，一般取5m/s，大跨越和高塔可取7～10m/s。风向对架空线的振动有很大影响。当风向与架空线的夹角在45°～90°之间，可以观察到架空线的稳定振动。当夹角在30°～45°之间，振动的时间较短，且时有时无而不持续。当夹角小于20°时，由于风输入的能量不足，基本上观察不到架空线的振动。 二、地形和地物的影响风速的均匀性与方向的恒定性，是保持架空线持续振动的必要条件。当线路通过开阔的平原地区，其地面的粗糙度小，对气流的扰乱作用小，气流的均匀性和方向性均不容易受到破坏，所以容易使架空线持续稳定振动。若地形起伏错综，地面粗糙度加大，破坏了气流的均匀性和方向的恒定性，因而架空线不易振动或作持续振动，而且振动强度降低。三、架空线结构和材料的影响1．架空线截面形状和表面状况的影响：圆形截面易形成卡门旋涡，引起振动；表面愈光滑，愈易微风振动。2．架空线股丝、股数和直径的影响：股数和层数多，自阻尼作用强，消耗更多能量使之不易振动或降低振动强度；截面积相同，股数愈则股线直径必然小，在同一允许振动应力值下，股线直径小的允许的弯曲幅值较大；但直径越小，疲劳断股的比例越高。 四、档距长度和悬挂高度的影响一般认为，风输给架空线的能量与档距长度成正比，即档距越大，风输入能量就越大。同时档距增大，半波数凑成整数的机率也增加。此外，档距长度增大，架空线悬挂高度随之增高，振动风速范围上限也相应提高。架空线离地愈高，气流的均匀性受地面粗糙度的干扰影响愈小。由于可致振动的风速范围加大，使得架空线发生振动的机率增加，同时也使架空线的振频与振幅加大。此风速上限值，可按下列经验公式计算（m/s）（10−17）3．架空线材料的影响：架空线所用材料的重量小，其振动严重：加速度大，振动频率高。4．分裂导线和间隔棒的影响：分裂导线，改变气流状况，削弱了振动能量；间隔棒的阻尼，增大能量消耗；间隔棒对子导线牵制。 五、悬挂体系的影响架空线通过绝缘子串与杆塔横担相连，其阻尼对架空线的振动有很大影响。振动时，绝缘子串各元件间产生相对位移和摩擦，横担产生变形，消耗振动能量，减轻了振动的危害。运行实践表明，悬垂串和针式绝缘子相比，刚度较小的木杆和刚度大的铁塔相比，刚度较小的横担端部和刚度较大的杆顶相比，酒杯铁塔的边横担和中横担相比，前者的架空线振动强度小，断股数少。1．对振动频率的影响从可以明显看出，张力T0增大，频率增高，振动次数多。如果以耐振次数衡量架空线疲劳极限，则其疲劳寿命短了，这对线路长期运行是不利的。六、架空线张力的影响 2．对疲劳极限的影响静态应力：架空线张拉应力，线股绞制后产生的残余应力，架空线弯曲所产生的弯曲应力等。动态应力：架空线的振动引起，对架空线的影响远大于静态应力，是引起架空线断股的主要原因。提高架空线张力，容易使其过早发生疲劳而导致断股或断线，对线路运行是不利的由古德曼（Goodman）图知—抗拉强度。—静态平均应力；—静态应力为零时的疲劳极限应力；—作用下的疲劳极限应力； 第四节微风振动强度的表示方法根据能量平衡原理，当架空线系统的阻尼消耗的能量与风输入系统的能量相等时，微风振动的幅值趋于稳定。一、采用振动角表示1．架空线的振动角架空线微风振动波在整个档距呈驻波形式，其离开平衡位置的位移大小，在档距和时间上都可近似视为按正弦规律变化。波峰（波腹）和节点的位置不变。节点的角度位移称为振动角，可用节点处的振动波斜率来表示。 由于线夹出口处的交变动应力最大，因此振动强度以线夹出口处的振动角大小来衡量。架空线上线夹出口附近任一点x处的振幅，根据式（10−11）可写为（10−19）最大振幅即半波中点的位移振动波的波长距线夹出口处的距离振动波的角频率其斜率即为振动角的正切在线夹出口处x=0，所以（10−20） 在悬挂点附近，即当x很小时，振幅，则（10−22），所以从上式看到，架空线振动角和时间t有关，在sinωt=1时有最大值（10−21）上式决定的振动角αm表示了振动的严重情况，可作为振动强度的表征参数。显然αm愈大，架空线在线夹出口处的弯曲程度愈严重，弯曲动应力也愈大，架空线也就愈容易产生断股。 2．振动角的允许值振动角的允许值理应按照动态应力的允许值确定，即应根据架空线线股的疲劳应力极限来确定。但直至目前为止，还没有简单实用的二者之间关系的计算公式，因此振动角的允许值是依据运行经验和试验确定的。振动角的允许值可参考下表。平均运行应力（抗拉强度的﹪）振动角允许值≤2510"＞255"在不采用防振措施时，实际工程中的振动角一般可达25"～35"。测量振动时，国际上规定以距线夹出口89mm（3.5英寸）处的振幅A89作为测量标准。此时（10−23） 二、采用动弯应变表示动弯应变与动弯应力成正比，动弯应变比振动角更能直接反映出架空线弯曲动应力的大小。A89与动弯应变之间可看为线性关系。测试表明，A89给定时架空线在线夹处的弯曲斜率，接近于均布荷载p作用下、末端挠度为A89、长为l=89mm的悬臂梁。根据材料力学有关公式，这种悬臂梁的固定端弯矩末端挠度设其外表面到弯曲中性层的距离为C，则其固定端的最大弯曲应变为 架空线外表面到弯曲中性层的距离C处于架空线半径与线股半径之间。测试表明，在A89不大于0.38mm时，若取架空线外层线股的半径即取C=0.5d，需在上式中乘以1.4的系数，所以测振常用的动弯应变计算式为（10−23）有文献指出，上式可能会有50%的误差，常数354随频率、振幅A89、张力和刚度等因素变化，建议对钢芯铝绞线取540，对大跨越各种导线取500。架空线材料允许动弯应变（×10−6）硬铝线、耐热合金线±100高强度铝合金线±120高强度耐热铝合金线±1201号铝合金线±150镀锌钢绞线±400 第五节微风振动的防振设计线夹出口处的架空线疲劳破坏最为严重。主要原因是：（1）线夹出口处的架空线始终是一个节点，振动角大；（2）线夹转动不灵活，容易形成死点，振动波不容易通过线夹传向相邻档。（3）悬点处架空线具有较大的静应力，允许的疲劳极限应力较低，最容易疲劳破坏引起断股甚至断线，或造成金具损坏。架空线微风振动的强度超过允许水平（如疲劳寿命40年）时，必须采取防振措施降低动弯应力和振动持续时间，以保护线夹出口处的架空线。 一、常用防振措施1．防振锤防振锤通过其线夹固定于架空线上，当架空线发生振动时，防振锤上下运动。耗能原理：（1）其钢绞线内摩擦，消耗大部分振动能量；（2）空气对重锤的阻尼，消耗一部分能量；（3）防振锤线夹处消耗和反射一部分能量。架空线系统消耗能量的增加，使微风振动的强度降低。 2．阻尼线在架空线悬垂线夹两侧或耐张线夹出口一侧，装上与架空线同型号或其它型号的单根线或部分双根线并在一起的连续多个花边，起阻尼防振作用，这些花边称为阻尼线。阻尼线通常与防振锤配合，用于输电线路大跨越。（a）垂直悬挂；（b）交叉悬挂 同防振锤比较，阻尼线的主要特点是：（1）重量轻，不容易在固定点形成“死点”；（2）取材方便，且便于通过调整花边改变固有频率，其固有频率较多；（3）在高频时，其耗能效果较防振锤好，但在低频时不如防振锤；（4）阻尼线的耗能特性曲线随频率变化出现非常凹凸的现象，在曲线的谷底点上消耗能量相当小，在小振幅时消耗能量急剧降低。防振锤和阻尼线防振具有互补性，大跨越多采用防振锤与阻尼线联合防振。 3．护线条目前导线上广泛采用的护线条，是用具有良好弹性的铝合金线股制成的螺旋形预绞丝。将护线条缠在导线上，置于悬垂线夹中。安装护线条后，由于加大了导线断面惯性矩，在同样的外力作用下，挠度减小，应变和应力减小，导线受力状况得到改善，一般可减小动弯应力20%～50%。现行线路的平均运行应力高，振动比较严重，单纯用护线条是不够的。护线条一般以护线为主，兼起防振作用。4．合理选择架空线的平均运行应力限制架空线运行应力，可以降低悬点静应力，有利于架空线的防振，因此设计规程中，对合理选择平均运行应力作了规定（表10−4）。其它防振办法：避开易振区、柔性横担、偏心线夹、防振线夹，打背线，自阻尼导线等。 需要时，安装设计内容：防振锤的型号、安装个数和安装位置等。1．防振锤型号的选择由于导线和地线的直径和单位重量不同，在使用中的悬挂高度、应力、档距也不同，风输入的能量不同，因此其振动幅值、振频范围等就有差异，不可能用一种型号的防振锤来解决所有架空线的振动问题。防振锤与架空线的配合。二、防振锤的安装设计是否需要？情况防振措施平均运行应力的上限（抗拉强度﹪）钢芯铝绞线钢绞线档距不超过500m的开阔地区不需要1612档距不超过500m的非开阔地区不需要1818档距不超过120m不需要1818不论档距大小护线条22—不论档距大小防振锤（阻尼线）或另加护线条2525 2．防振锤个数的选择架空线的振幅很小或振动时间很短，不需要安装防振锤。随着档距的增大和平均运行应力上限的提高，振动随之严重，需要采取相应的防振措施，在档距的两端各安装一个防振锤。对于300m以上的较大档距，一端装一个标准防振锤不足以将振幅降低到规定的水平，需要安装多个（一般1～3个）防振锤。对于大跨越，有时甚至达到6～7个。分裂导线采用阻尼间隔棒时，档距在500m及以下可不再采用其他防振措施。防振锤型号FD−1FD−2FD−3FD−4FD−5架空线截面（mm2）35～5070～95120～150185～240300～400防振锤型号FD−6FG−35FG−50FG−70FG−100架空线截面（mm2）500～630355070100档距范围（m）防振锤个数架空线直径d（mm）123d＜12≤300＞300～600＞600～90012≤d≤22≤350＞350～700＞700～100022＜d＜37.1≤450＞450～800＞800～1200 3．防振锤安装位置的计算防振锤最好安装在波腹点附近位置。但频率和波长随风速大小和应力大小而变化；在振动风速范围内，波长在最大值和最小值之间变动。防振锤的安装位置应照顾到最长和最短波时都能起到一定的防振作用。不同的观点：（1）安装数量基本上与档距的长度成正比，再大的档距亦应如此。（2）半档防振方法。（3）档距每端安装的防振锤数量不应超过两个，且频率特性应不同；如果档距很大，仍不能将振幅限制到安全值以下，则应采用“档距中央阻尼”的其它方法解决。 根据图示，防振锤的安装位置S0对最长波和最短波均有防振作用，其它波的第一个节点位于最短半波长和最长半波长之间，均大于S0，故对其它波而言，防振锤安装在S0位置将比最长波和最短波更接近于波腹，防振作用将会更好。如果将防振锤装在对最长波最有利的位置S点处，效果怎样？ 防振锤的具体安装位置应在最长波波腹的前半部和最短波波腹的后半部，并使两种波的相角互补，即（10−24）而，代入式（10−24），整理后得（10−25） 令架空线振动频率等于卡门旋涡频率，得到最长半波长和最短半波长为，（10−26）当时，式（10−25）变为，这意味着置防振锤于最短波的波节点上,为使防振锤仍有一定作用，可引入系数进行调整。通常为（10−27）因此有时用架空线的平均运行张力Tcp代替最高和最低气温下的张力TN和TM计算半波长，此时防振锤的安装距离为（10−28）在线路运行中，出现最高气温和最低气温的时间不多，且风速远较架空线张力对波长的影响大，而大档距架空线在最高和最低气温下的张力变化并不很大防振锤的安装距离S0，通常是指从线夹出口到防振锤固定线夹中心间的距离。但对中心转动式悬垂线夹，可以悬垂线夹中心为起点；对轻型耐张线夹，以线夹连接螺栓中心为起点；对重型耐张线夹，则需以线夹出口处为起点。 4．多个防振锤的安装位置安装多个防振锤时，仍以最大限度地抑制振动为原则确定安装位置。有等距离安装和不等距离安装两种。（1）等距离安装等距离安装即各相邻防振锤的间距均等于S0，第i个防振锤的中心距线夹出口处的距离Si为（10−29）这种安装方式，第1个防振锤位于第1个最短半波内，第i个防振锤位于第i个最短半波内，防振效果较好。但有可能n个防振锤均位于第1个最长半波内，使n个防振锤的总质量远大于该段架空线的质量从而该段架空线不再振动，防振效果不好。简单，常用。 （2）不等距安装具体的安装方法目前尚未统一。若每端安装n个同型防振锤，可将防护范围等比例的分为n段，即其中，，对间的安装位置仍按式（10−25）的原则计算，不难导出第i个防振锤的安装距离为（10−30）采用两个同型防振锤时的安装距离，可由下式确定（10−31） 三、阻尼线的安装设计1．阻尼线的选材阻尼线宜采用比被保护架空线较轻的绞线，股径细、股数和层数多的较好，因为这种绞线的自阻尼性能好，能较多地吸收能量；弯曲刚度较小，可以获得较低的共振频率；各阶振频率间隔小，能与更多的架空线固有频率发生共振，因此其防振效果较好。国外也有采用挠性好的钢丝绳作阻尼线的，防振效果也很好。但连接点处钢丝绳的垂直重量最好不超过按架空线选配的防振锤的重量，以防止出现“死点”。 2．阻尼线花边的固有频率阻尼线的花边，可视为档距l和张力T0都很小、刚度为EJ的悬线。根据公式（10−14），其n阶固有频率为（10−32）阻尼线花边的固有频率与花边弦长的平方成反比。因此长花边用于防护低频振动，中花边用于防护中频，短花边用于防护高频。3．花边数、花边弧垂花边的个数随档距的增加而增多，一般最少3个，多则达5～6个。花边的弦长一般不等，由线夹处向档距中央花边弦长递减。花边弧垂的大小对防振效果影响不大。