数学建模送货路线设计问题 28页

送货路线设计问题摘要：本文主要讨论的是送货路线的设计问题。总体的解题思路是将问题中的地点、路线分别抽象成数学中的点、线，然后利用图论的相关知识理论来考虑这些问题。最后，设计方法程序，并利用Matlab运行，解决问题。问题一要求根据1-30号货物设计一条最快的送货路线，由于货物的总质量mzong和总体积vzong（mzong=48.5000;vzong=0.8800）均未超出最大限度50和1，所以，该问题可转化成求最短路问题。解决方法：首先，写出每个点的带权邻接矩阵；然后，运用Floyd求任意两点间的最短距离；最后，用H圈构造运算法,并通过矩阵翻转的二边逐次修正法，得到最短距离和最快完成路线图，如下:o→18→13→24→31→27→39→34→40→45→49→42→43→36→38→32→23→16→14→17→21→26→olucheng=5.4707e+004米t=lucheng/1000*v+t*21/60=3.3295小时问题二设计一条路线，要求在时间允许的条件下，使总路程最小。解决思路是利用问题一中的方法，结合每个货物的时间限制，最终得到路线图，如下：o→18→13→24→31→27→39→34→40→45→49→42→43→38→36→32→23→16→14→17→21→26→olucheng2=5.4707e+004t2=lucheng2/1000*v+t*21/60=3.3295小时问题三将1-100号货物全部送到指定地点，mzong=148，vzong=2.8，显然不能一次性送到。解题思想是根据仓库到各个点的最小距离将地点分为三部分，分别派送。分完组后在利用第一问的思想给予优化求出最佳的H圈.得到的送货路线分别为:第一组路线：o→26→31→27→39→27→36→45→40→47→40→50→49→42→43→38→35→32→23→17→21→o；第二组路线：o→26→31→34→40→37→41→44→48→46→33→28→30→22→20→22→29→25→19→24→31→26→o；第三组路线：o→21→17→23→16→14→9→10→7→1→6→1→8→3→4→2→5→15→12→11→13→1811→o。送货时间为:t3=lucheng/1000*v+t*100/60=10.563小时关键词：图论带权邻接矩阵Floyd算法最优Hamilton圈二边逐次修正一、问题重述现今社会网络越来越普及，网购已成为一种常见的消费方式，随之物流行业也渐渐兴盛，每个送货员需要以最快的速度及时将货物送达，而且他们往往一人送多个地方，请设计方案使其耗时最少。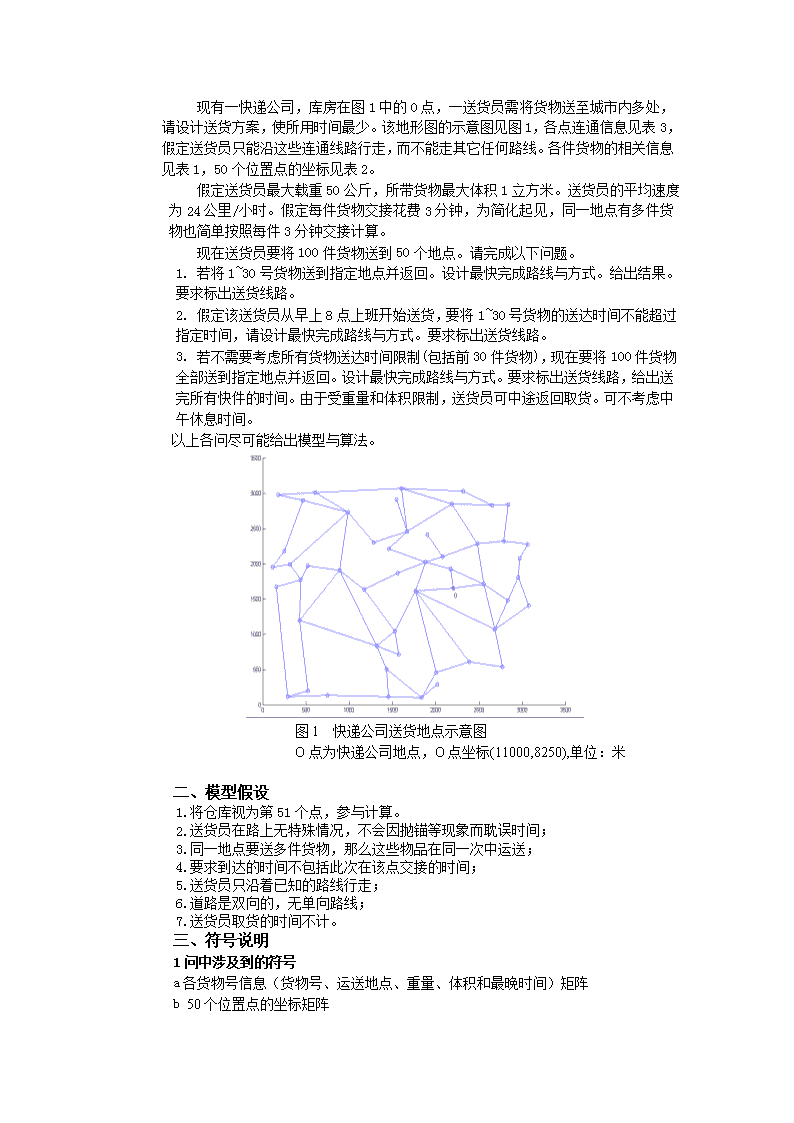 现有一快递公司，库房在图1中的O点，一送货员需将货物送至城市内多处，请设计送货方案，使所用时间最少。该地形图的示意图见图1，各点连通信息见表3，假定送货员只能沿这些连通线路行走，而不能走其它任何路线。各件货物的相关信息见表1，50个位置点的坐标见表2。假定送货员最大载重50公斤，所带货物最大体积1立方米。送货员的平均速度为24公里/小时。假定每件货物交接花费3分钟，为简化起见，同一地点有多件货物也简单按照每件3分钟交接计算。现在送货员要将100件货物送到50个地点。请完成以下问题。1.若将1~30号货物送到指定地点并返回。设计最快完成路线与方式。给出结果。要求标出送货线路。2.假定该送货员从早上8点上班开始送货，要将1~30号货物的送达时间不能超过指定时间，请设计最快完成路线与方式。要求标出送货线路。3.若不需要考虑所有货物送达时间限制(包括前30件货物)，现在要将100件货物全部送到指定地点并返回。设计最快完成路线与方式。要求标出送货线路，给出送完所有快件的时间。由于受重量和体积限制，送货员可中途返回取货。可不考虑中午休息时间。以上各问尽可能给出模型与算法。图1快递公司送货地点示意图O点为快递公司地点，O点坐标(11000,8250),单位：米二、模型假设1.将仓库视为第51个点，参与计算。2.送货员在路上无特殊情况，不会因抛锚等现象而耽误时间；3.同一地点要送多件货物，那么这些物品在同一次中运送；4.要求到达的时间不包括此次在该点交接的时间；5.送货员只沿着已知的路线行走；6.道路是双向的，无单向路线；7.送货员取货的时间不计。三、符号说明1问中涉及到的符号a各货物号信息（货物号、运送地点、重量、体积和最晚时间）矩阵b50个位置点的坐标矩阵 c互通点信息矩阵d任意两相通两点间距离e对应两相通两点间距离e1对e进行去重后得到的矩阵f带权邻接矩阵D任意两点间最小距离矩阵u初始H圈mzong货物的总质量vzong货物的总体积luxian最短路线lucheng最小路程t1最短时间t货物交接时所需时间（3分钟）v送货员的行驶速度(24千米每小时)2问中涉及到的符号luxian2最短路线lucheng2最小路程t2最短时间3问中涉及到的符号luxian3最短路线lucheng3最小路程t3最短时间D3分组矩阵四、问题的分析与模型的建立将快递网图中，每个投递点看作图中的一个节点，各投点之间的公路看作图中对应节点间的边，各条路的长度（或行驶时间）看作对应边上的权，所给快递网就转化为加权网络图，问题就转化为在给定的加权网络图中寻找从给定点0出发，行遍所有顶点至少一次再回到O点，使得总权（路程或时间）最小，此即最佳推销员回路问题。1)问题一是需将30个货物送达21个固定点并返回，O点和另外21个点构成了一个典型的最短路问题。即先利用Floyd计算两点间的最短距离，再随机构造哈密顿圈，利用优化算法对此H圈优化，使H圈的权最小。2)问题二本小问是在一问的基础上加入时间的限制，解题思想是以第一问的过程为基础，从随机产生的H圈中选出符合时间要求的多条路线，再从中学出事的路程权重最小的路线。并检验其是否符合时间的要求。3)问题三主要是对路线的分组,分组后检验，调整使得每组货物质量小于50kg，体积小于1m3，然后利用问题一，解出每组的最佳H圈。五、模型的分析与求解1.5.1由附录1给定的数据知，前30号货物由于货物的总质量mzong和总体积vzong分别为48.5和0.88均未超出最大限度50和1，显然送货员能够一次带上所有货物到达各送货点，且货物要送达总共为21个，如下：13,14,16,17,18,21,23,24,26,27,31,32,34,36,38,39,40,42,43,45,49本模型运用图论中Floyd算法与最佳Ｈ圈中的相关结论，建立了关于该类问题的优化模型，将出发点O和21个送货点结合起来构造完备加权图。 用矩阵翻转来实现二边逐次修正，求最佳哈密尔顿圈（H圈）。由完备加权图,确定初始H圈,列出该初始H圈加点序边框的距离矩阵,然后用二边逐次修正法对矩阵进行“翻转”,就可得到近似最优解的距离矩阵,从而确定近似最佳H圈。由于用矩阵翻转方法来实现二边逐次修正法的结果与初始圈有关，故为了的到得到较优的计算结果，在用MATLAB编程时，随机搜索出200个初始H圈。在所有H圈中，找出权最小的一个，即要找的最佳H圈的近似解。最佳H圈的近似解min｛H0，H1，H2,…H99｝送货路线：o→18→13→24→31→27→39→34→40→45→49→42→43→36→38→32→23→16→14→17→21→26→o送货时间：lucheng=5.4707e+004米t=lucheng/24000+3*21/60=3.3295小时1.5.2本小问是在一问的基础上加入时间的限制，解题思想是以第一问的过程为基础，从随机产生的H圈中选出符合时间要求的多条路线，即选择符合每个点时间要求的最佳H圈。为了更有针对性，可将一问的最佳路线作为初始的H圈进行计算。得到结果，如下：o→18→13→24→31→27→39→34→40→45→49→42→43→38→36→32→23→16→14→17→21→26→olucheng2=5.4707e+004t2=lucheng2/24000+3*21/60=3.3295小时 1.5.3现根据距离分组，在调整，然后求解。51号到各个地点的最小距离如下：1234567891010068162961046714004165631136281008509777580921112131415161718192069656752529550941155874933621218269681341721222324252627282930179711918539547098934139239971422310820132053132333435363738394029296707155495254762446778975621457776885414243444546474849501157797518833139437860143129216158061172299280→26→31→27→39→27→36→45→40→47→40→50→49→42→43→38→35→32→23→17→21→0；0→26→31→34→40→37→41→44→48→46→33→28→30→22→20→22→29→25→19→24→31→26→0；0→21→17→23→16→14→9→10→7→1→6→1→8→3→4→2→5→15→12→11→13→18 11→0。计算三个区域各自送货员走的总路程:142173.27m239894.58m351440.73m计算时间:(51440.73+39905.76+42173.27)/24000+3/60*100=10.563小时六、模型的不足及改进的方向不足：由于数据量大，且最佳H圈与原始圈的选取有关，只能去近似最佳圈，因此对于第二问随机性很强，只能多设置一下循环次数，以求精确。第三问的手动画图、分组比较麻烦，要尝试多次才能找出符合要求的点。参考文献【1】赵静、但琦，数学建模与数学实验（第3版）高等教育出版社【2】姜启源、谢金星、叶俊，数学模型，北京：高等教育出版社，2003相关程序数据图1快递公司送货地点示意图O点为快递公司地点，O点坐标(11000,8250),单位：米表1各货物号信息表货物号送达地点重量(公斤)体积(立方米)不超过时间1132.500.03169：002180.500.03549：003311.180.02409：304261.560.035012：005212.150.030512：00 6141.720.010012：007171.380.010912：008231.400.042612：009320.700.048112：0010381.330.021910：1511451.100.02879：3012430.950.022810：1513392.560.059512：0014452.280.03019：3015422.850.019010：1516431.700.078210：1517320.250.041212：0018361.790.018412：0019272.450.044512：0020242.930.04209：0021310.800.01089：3022272.250.001812：0023261.570.021012：0024342.800.01039：3025401.140.01559：3026450.680.03829：3027491.350.014410：1528320.520.002012：0029232.910.048712：0030161.200.042912：003111.260.02503221.150.05013331.630.04833441.230.00063551.410.03873660.540.00673770.700.01293880.760.03463992.140.008740101.070.012441111.370.051042122.390.042843130.990.004844141.660.049145150.450.020946162.040.009847171.950.032448182.120.055449193.870.026250202.010.032451211.380.041952220.390.000153231.660.050254241.240.053455252.410.001256261.260.0059 57270.420.022458281.720.058059291.340.037260300.060.040261310.600.027462322.190.050363331.890.049464341.810.032565351.000.005566361.240.017767372.510.036168382.040.011069391.070.044070400.490.032971410.510.009472421.380.045573431.310.012174441.260.000575450.980.041376461.350.024177472.120.023078480.540.054279491.010.056680501.120.028481250.790.001182462.120.049283322.770.003484232.290.005485200.210.049086251.290.008887191.120.024988410.900.003889462.380.043490371.420.002091321.010.030092332.510.013393361.170.002094381.820.030895170.330.034596110.300.017297154.430.053698120.240.005699101.380.017510071.980.0493表250个位置点的坐标位置点X坐标(米)Y坐标(米)19185500214455603727057043735670526209956100801435 71002522808716025259138452680101193530501178503545126585418513763052001413405532515212559751615365704517141657385188825807519585581652078083552112770856022220088352314765905524779093302544359525261086096352710385105002856597652925809865301565995531939510100321483510365331250109003472801106535153051137536123901141537641011510381391511610399510120504083451230041493013650421326514145431418014215443030150604510915142354623301450047773514550488851488049115751516050801015325表3相互到达信息序号位置点1位置点21132183220424538634 7428515952106111718127113812149141591016101817107181112191213201225211215221318231319241311251418261416271417281421291522301525311623321723331831341924352022362126372136382117392230402317412431422541432519442529452731462833472922483028493041503126513134523235533223543346553328563440573538583645593627603740 61383662392763403464404565414466413767414668424369424970433871444872445073455074454275464876474077484478495079494280504081O1882O2183O26程序问题一的程序1.%作图，标号，标距离clc;a=[%货物信息数据113.00002.50000.03169.0000218.00000.50000.03549.0000331.00001.18000.02409.3000426.00001.56000.035012.0000521.00002.15000.030512.0000614.00001.72000.010012.0000717.00001.38000.010912.0000823.00001.40000.042612.0000932.00000.70000.048112.00001038.00001.33000.021910.15001145.00001.10000.02879.30001243.00000.95000.022810.15001339.00002.56000.059512.00001445.00002.28000.03019.30001542.00002.85000.019010.15001643.00001.70000.078210.15001732.00000.25000.041212.00001836.00001.79000.018412.0000 1927.00002.45000.044512.00002024.00002.93000.04209.00002131.00000.80000.01089.30002227.00002.25000.001812.00002326.00001.57000.021012.00002434.00002.80000.01039.30002540.00001.14000.01559.30002645.00000.68000.03829.30002749.00001.35000.014410.15002832.00000.52000.002012.00002923.00002.91000.048712.00003016.00001.20000.042912.0000311.00001.26000.02500322.00001.15000.05010333.00001.63000.04830344.00001.23000.00060355.00001.41000.03870366.00000.54000.00670377.00000.70000.01290388.00000.76000.03460399.00002.14000.008704010.00001.07000.012404111.00001.37000.051004212.00002.39000.042804313.00000.99000.004804414.00001.66000.049104515.00000.45000.020904616.00002.04000.009804717.00001.95000.032404818.00002.12000.055404919.00003.87000.026205020.00002.01000.032405121.00001.38000.041905222.00000.39000.000105323.00001.66000.050205424.00001.24000.053405525.00002.41000.001205626.00001.26000.005905727.00000.42000.022405828.00001.72000.058005929.00001.34000.037206030.00000.06000.040206131.00000.60000.027406232.00002.19000.05030 6333.00001.89000.049406434.00001.81000.032506535.00001.00000.005506636.00001.24000.017706737.00002.51000.036106838.00002.04000.011006939.00001.07000.044007040.00000.49000.032907141.00000.51000.009407242.00001.38000.045507343.00001.31000.012107444.00001.26000.000507545.00000.98000.041307646.00001.35000.024107747.00002.12000.023007848.00000.54000.054207949.00001.01000.056608050.00001.12000.028408125.00000.79000.001108246.00002.12000.049208332.00002.77000.003408423.00002.29000.005408520.00000.21000.049008625.00001.29000.008808719.00001.12000.024908841.00000.90000.003808946.00002.38000.043409037.00001.42000.002009132.00001.01000.030009233.00002.51000.013309336.00001.17000.002009438.00001.82000.030809517.00000.33000.034509611.00000.30000.017209715.00004.43000.053609812.00000.24000.005609910.00001.38000.017501007.00001.98000.04930];b=[%货物坐标数据1918550021445560 3727057043735670526209956100801435710025228087160252591384526801011935305011785035451265854185137630520014134055325152125597516153657045171416573851888258075195855816520780835521127708560222200883523147659055247790933025443595252610860963527103851050028565976529258098653015659955319395101003214835103653312501090034728011065351530511375361239011415376410115103813915116103995101205040834512300414930136504213265141454314180142154430301506045109151423546233014500 4777351455048885148804911575151605080101532551110008250];c=[%连通数据11321832204245386347428515952106111718127113812149141591016101817107181112191213201225211215221318231319241311251418261416271417281421291522301525311623321723331831341924352022362126372136 382117392230402317412431422541432519442529452731462833472922483028493041503126513134523235533223543346553328563440573538583645593627603740613836623927634034644045654144664137674146684243694249704338714448724450734550744542754648764740774844784950794942805040815118 825121835126];fori=1:83%求相连通的点之间的距离x(i)=b(c(i,2),2);x(i+1)=b(c(i,3),2);y(i)=b(c(i,2),3);y(i+1)=b(c(i,3),3);d(i)=sqrt((x(i)-x(i+1)).^2+(y(i)-y(i+1)).^2);endd;e=[c,d"];%对应点之间的距离矩阵plot(b(a(:,2),2),b(a(:,2),3),"ro")text(11000,8250,"O库房");forj=1:81text(b(a(j,2),2),b(a(j,2),3),num2str(a(j,2)));endholdonfori=1:83plot(b(c(i,2:3),2),b(c(i,2:3),3),"b")x=b(c(i,2:3),2);x1=sum(x)/2;y=b(c(i,2:3),3);y1=sum(y)/2;text(x1,y1,num2str(e(i,4)))end2.%H圈函数function[a,b,s,s1]=h(e)%e为按照初始H圈点的顺序组成的含点序边框的距离矩阵n=size(e);%求出距离矩阵的维数.a=ones(25,25);b=ones(25,25);fori=2:n-2;%有一个顺序的外框,所以循环从2开始到n-2.forj=i+1:n-2;ife(i,j)+e(i+1,j+1)